physicslovers. com

STRESS-STRAIN CURVE:

Published by : Junaid Rashid Student at central university of kashmir, department of physics

• Stress is defined as the deforming force per unit area. Numerically it is given as; Stress= Force/Area. It’s S.I unit is newton/metre squared.

• Strain is defined as the ratio of change in the configuration to the original configuration of the body.

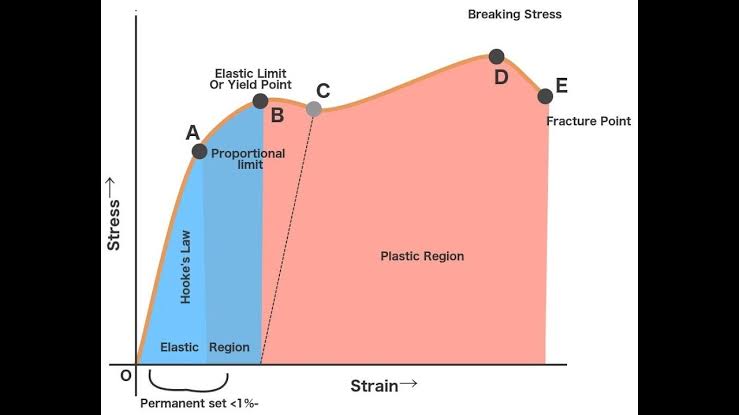
• At point ‘o’ both stress and strain are equal to zero.

• When stress is applied on a body, strain is produced in it. If we remove stress, strain also disappears and increase in stress causes increase in strain in the body.

• The maximum value of stress upto which strain is proportional to stress is called as proportional limit. In this region, body is perfectly elastic i.e, Hooke’s law is valid.

• Point ‘A’ is called as proportional limit and region ‘oA’ is known as proportional region.

• ‘AB’ region is curved which means that stress is no more proportional to strain. However if the deforming load is removed at any point upto ‘B’, the curve retraces its original path along ‘BAo’ which implies that wire attains it’s original length. Thus upto point ‘B’, forces are conservative in the sense that when material returns to it’s original configuration, the work done in producing the deformation is completely recovered.

• Region ‘oB’ is called as elastic region and point ‘B’ is called elastic limit or upper yield point. Stress corresponding to point ‘B’ is known as yield strength.

• Upper yield point (B) represents the maximum stress upto which material is deformed elastically i.e, though material undergoes deformation but once the deforming force is removed, body regains it’s original configuration.

• Beyond upper yield point ‘B’, strain increases more rapidly than stress and even if load is completely removed at any point between ‘B’ and ‘C’, body doesn’t retrace it’s original path but retraces another path represented by a dotted line in the graph and wire is said to be in permanent set.

• The fact that stress-strain curve is not retraced on reversing the strain is called as elastic hysteresis.

• Point ‘C’ is called as lower yield point representing the stress at which deformation is completely plastic.

• Point ‘D’ represents the breaking stress for the given material. Breaking stress is the maximum stress which a material can withstand before it finally breaks. It is important to mention here that breaking stress of a given material is independent of it’s dimensions like length and area but depends on the nature of the material.

• Breaking stress is also called the tensile strength or ultimate strength of the material.

• After point ‘C’, material experiences high rate of plastic deformation and once the material yields, it begins to strain harden which increase its strength. This increase in strength is the result of strain hardening and is observed between yield point (C) and ultimate point (D). The ratio of ultimate strength to yield strength is called as strain hardening ratio and is used to measure the degree of strain hardening in the material.

• Finally with further increase in the deforming load, wire breaks at point ‘E’ called as breaking point or fracture point.

• The region between ‘B’ and ‘D’ is known as plastic region and the deformation as plastic deformation. Plastic deformation is an irreversible deformation of a material.

• It is quite important to note that stress is not a vector quantity but it is a tensor. The tensor nature of stress can be explained as follows:

• The stress acting on any surface of a body can be resolved into its three mutually orthogonal components. One component is along the normal to the surface representing normal stress while remaining two components are tangential to the surface representing shear or tangential stress. Normal stress tends to change the volume and is resisted by the bulk modulus of the material while shear stress tends to deform the material without changing it’s volume and is resisted by body’s shear modulus.

• Consider an internal point ‘P’. The stress state at this point can be represented by an infinitesimal cube with three stress components on each of it’s six sides- one normal and two tangential. Since each point in the body is under static equilibrium i.e, net force acting on each point is zero hence only nine stress components, three from each plane are required to describe the stress state at any arbitrary point ‘P’. In determinant form the stress state at point ‘P’ can be represented by a matrix of three rows and three columns as shown below.

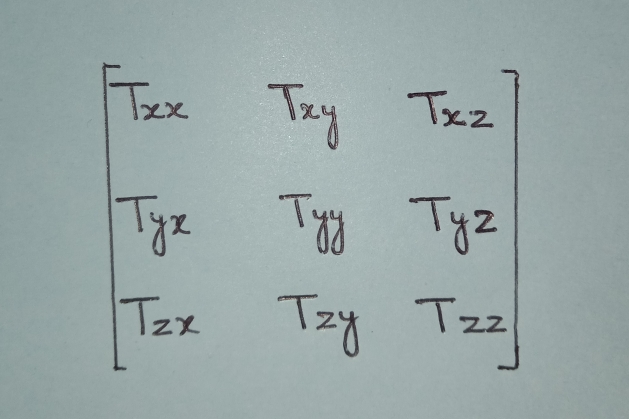
• As a consequence of static equilibrium, the shear stresses along the diagonal are identical i.e, Txy= Tyx ,Tyz=Tzy , Tzx=Txz

• This grouping of nine stress components in a matrix is called as stress tensor or stress matrix.

• The subscript notations used for nine stress components have the following meanings: first subscript represents the direction of surface normal upon which stress is acting while the second subscript represents the direction of stress component.

• From the above discussion, we conclude that stress is a second order tensor as it is a quantity associated with two directions.That is why each component is having two subscripts. On the other hand, vector quantity is a first order tensor as it is associated with only one direction due to which each component of a vector quantity has only one subscript. Accordingly, a scalar quantity is a zero order tensor as it is direction independent and gives only magnitude.

THE END..

HYSTERESIS CURVE: Brief discussion.

Published by: Junaid Rashid. student at central university of Kashmir department of physics.

Hysteresis is a property of ferromagnetic substances.
Hysteresis loop is a curve between magnetising field H and magnetisation ( I or M) .Sometimes it is drawn between H and B (induced flux density which gives the measure of M)
Hysteresis Loop is generated by measuring magnetic flux coming out of ferromagnetic substance while changing the external magnetising field.
Initially, the external magnetising field is zero hence magnetisation is also equal to zero.
Now with the increase in magnitude of H, magnetisation M also increases though not proportionally and attains it’s maximum value at point “a” Called as saturation point. Beyond saturation point, increase in H has no effect on the magnitude of M.
Now, on decreasing the value of H, magnetisation also decreases. However when H=0 magnetisation is not equal to zero implying that material has retained some magnetism even after the removal of external magnetising field called as residual magnetism or remnant magnetism denoted by “ob”.
This property of ferromagnetic substances to retain magnetism even when external magnetising field ceases is called as retentivity.
With increase in external magnetising field towards negative side(decrement),M decreases and becomes zero at a particular value of H.
The amount of magnetising field required to destroy the residual magnetism of ferromagnetic substance is called coercivity or coercive force denoted by “oc” In hysteresis loop.
With further increase in H towards negative side(decrement), material is magnetised in opposite direction and magnetisation attains maximum value at point “f”
At point “e”, H=0 but material has some residual magnetism(opposite direction) denoted by “oe”
Further when H is increased towards positive side(increment), magnetism decreases and becomes zero at point “d” Such that “od” represents positive coercive force.
With further increase in H, material gets magnetised in same direction as it was magnetised initially and attains maximum value at point “a” called as saturation point and the cycle is completed called hysteresis loop.
At every point of the loop, M lags behind H called hysteresis.
Summary of hysteresis loop: magnetisation (a), de-magnetisation (c) , magnetisation in opposite direction (f), de-magnetisation (d) and magnetisation (a)
It is worth mentioning that for a unique value of H, M is not unique because it depends on the history of the given sample.
When a ferromagnetic substance undergoes a cycle of magnetisation, energy is required to align the molecular dipoles in the direction of external magnetising field. On the contrary, when magnetising field is removed all the spent energy is not recovered back due to the fact that M doesn’t fall to zero when H=0. Hence there is energy loss.
Energy lost per unit volume of material in each cycle of hysteresis loop is directly proportional to area under hysteresis loop.Wider the hysteresis loop, more the energy loss and vice versa
Applications
Hysteresis loop is useful in practical world in the sense that it is used to differentiate between electromagnets and permanent magnets.
Electromagnets lose magnetism as soon as the external magnetising field is removed e.g soft iron. Magnetisation is temporary.
Permanent magnets on the other hand retain magnetism even after the removal of external magnetising field which means that magnetisation is permanent in this case. e.g Alnico(Al, Ni, Co, Cu) , Steel.
Use of soft iron in generators and transformers is based on the fact that it magnetize and de-magnetize fastly due to low value of Coercivity, and less area under hysteresis loop.

The End..

Introduce Yourself (Example Post)

This is an example post, originally published as part of Blogging University. Enroll in one of our ten programs, and start your blog right.

You’re going to publish a post today. Don’t worry about how your blog looks. Don’t worry if you haven’t given it a name yet, or you’re feeling overwhelmed. Just click the “New Post” button, and tell us why you’re here.

Why do this?

Because it gives new readers context. What are you about? Why should they read your blog?
Because it will help you focus your own ideas about your blog and what you’d like to do with it.

The post can be short or long, a personal intro to your life or a bloggy mission statement, a manifesto for the future or a simple outline of your the types of things you hope to publish.

To help you get started, here are a few questions:

Why are you blogging publicly, rather than keeping a personal journal?
What topics do you think you’ll write about?
Who would you love to connect with via your blog?
If you blog successfully throughout the next year, what would you hope to have accomplished?

You’re not locked into any of this; one of the wonderful things about blogs is how they constantly evolve as we learn, grow, and interact with one another — but it’s good to know where and why you started, and articulating your goals may just give you a few other post ideas.

Can’t think how to get started? Just write the first thing that pops into your head. Anne Lamott, author of a book on writing we love, says that you need to give yourself permission to write a “crappy first draft”. Anne makes a great point — just start writing, and worry about editing it later.

When you’re ready to publish, give your post three to five tags that describe your blog’s focus — writing, photography, fiction, parenting, food, cars, movies, sports, whatever. These tags will help others who care about your topics find you in the Reader. Make sure one of the tags is “zerotohero,” so other new bloggers can find you, too.